Colorindo Imagens Astronômicas em Python
Durante a SIFSC12 foi realizado um minicurso do CAIFSC baseado em um material que eu havia preparado para uma reunião do clube. Durante o curso eu prometi fazer uma postagem no blog detalhando esse material. E então cá estamos!
A proposta do curso é usar técnicas básicas de processamento de imagens para dar cor à imagens do James Webb Space Telescope(JWST). Para isso, vamos voltar um pouco e definir o que é uma imagem digital.
Imagens digitais
Imagens são um tipo de informação bastante comum na experiência humana. Por isso, é interessante reproduzir, mesmo que de forma simplificada, essa informação. Pinturas, fotos e, nas últimas décadas, imagens digitais são uma expressão desse interesse.
Imagens digitais são, de forma simplificada, representações de imagens que podem ser exibidas em um monitor e, consequentemente, que podem ser armazenadas em um computador(acho que nem preciso dizer que são praticamente todas que você vê todos os dias). Existe mais de uma forma de se armazenar uma imagem num computador, mas hoje vamos usar apenas uma: matrizes.
Imagine que você queria explicar ao seu computador o que é uma imagem. Lembre-se, o seu computador só entende números e possui memória limitada(ele só consegue guardar uma quantidade finita de números). Uma possibilidade seria dividir essa imagem em pequenos quadradinhos e atribuir números a esses quadradinhos. Esses quadradinhos seriam então elementos da imagem(em inglês picture element, ou pixel) e o número atribuido seria a intensidade desse pixel. A partir daí, basta guardar esses números em uma matriz nas posições corretas e agora temos uma forma de mostrar essa imagem ao seu computador!
Escala de cinza e RGB
Você talvez esteja se perguntando onde a cor entra nessa história(ou não). Bom, quando eu disse que cada posição da matriz recebe um valor de intensidade, na verdade eu estava falando de um tipo específico de imagem: imagens em escala de cinza(grayscale). Esse tipo de imagem de fato só representa variações de intensidade(claro ou escuro) e são representadas, geralmente, em preto e branco. Cada pixel então é um valor num intervalo $[0,I_{max}]$, quando esse valor é $0$ o pixel é preto e quando o valor é $I_{max}$ o pixel é branco. Na vida real, podemos ter qualquer valor de intensidade nesse intevalo, mas, como eu já disse, o computador tem memória finita, então temos que dividir esse intevalo de forma discreta. Quanto mais dividirmos esse intervalo, melhor podemos representar variações sutis de intensidade. Você já deve ter ouvido falar em cores 8-bits e 16-bits, pois bem, em 8-bits podemos ter $2^{8} = 256$ níveis de intensidade e em 16-bits podemos ter $2^{16} = 65536$. Sistemas modernos usam 24-bits ou mais, faça as contas!
Mas e as malditas cores? Bom, para isso, armazenamos em cada entrada da matriz mais de um número, cada um representando intensidades em escalas de cor diferentes(você pode imaginar que está misturando tinta e a intensidade representa a quantidade de tinta que vocês está misturando). Existem vários sistemas de cor, como o CMYK, utilizado em imagens com a finalidade de impressão e, o sistema utilizado nesse curso, o RGB, onde cada pixel armazena informação de três canais de cor(vermelho, verde e azul).
Imagens do JWST
O JWST capta imagens em escala de cinza. Sim, isso mesmo, o JWST, e telescópios em geral, captam imagens em preto e branco. Mas então como a NASA posta aquelas belas imagens todo dia no Instagram? Bom, é isso que viemos responder aqui.
O JWST capta sinais em infra-vermelho. Esses sinais passam por filtros que separam frequências específicas do espectro eletromagnético e então são “traduzidos” para frequências do intervalo visível do espectro. Podemos então pegar os sinais correspondentes à partes de frequência mais baixa e associar ao vermelho e então fazer o mesmo por todo o espectro. Uma vez tendo os sinais correspondentes ao vermelho, verde e azul, podemos criar imagens coloridas!
Simples? Pois é, tem alguns detalhes no meio dessa história, mas cuidaremos disso depois.
Imagens em Python
Agora que já sabemos a teoria(mais ou menos), podemos começar a botar a mão na massa! Para isso utilizaremos a internacionalmente aclamada linguagem de programação Python. Para fins didáticos, esse curso utilizará apenas as bibliotecas numpy, matplotlib e os, mas existem bibliotecas mais sofisticadas para processamento de imagem, como a scikit-image.
Vamos importar essas bibliotecas e abrir as imagens correspondentes à diferentes filtros do JWST:
1
2
3
4
5
6
7
8
9
10
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.gridspec as gridspec
import os
imgs = []#lista para armazenar as imagens
for img in sorted(os.listdir('./ngc3324/')):#para cada imagem no diretorio /ngc3324
if os.path.splitext(img)[1] == '.png':#se for um png
print(img)#printa o nome da imagem
imgs.append(plt.imread('./ngc3324/'+img))#guarda na lista de imagens
A biblioteca matplotlib oferece a função imread , que permite abrir imagens em vários formatos.
Para facilitar a visualização vamos criar uma função, mas não se preocupe com ela, é só um monte de “matplotlib-fu”:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def show_img(img_list, nrow, ncol):
fig = plt.figure(figsize=(5*(ncol+1), 5*(nrow+1)))
gs = gridspec.GridSpec(nrow, ncol,
wspace=0.05, hspace=0.0,
top=1.-0.5/(nrow+1), bottom=0.5/(nrow+1),
left=0.5/(ncol+1), right=1-0.5/(ncol+1))
idx = [(0,0), (0,1), (0,2), (1,0), (1,1), (1,2)]
for i in range(ncol*nrow):
ax = plt.subplot(gs[idx[i]])
ax.imshow(img_list[i], "gray")
ax.set_xticks([])
ax.set_yticks([])
Você pode então ver as imagens com:
1
show_img(imgs, 2, 3)#2 e 3 são o número de linhas e colunas
Muito emocionante, não? Não pare de ler, eu prometo que vai funcionar!
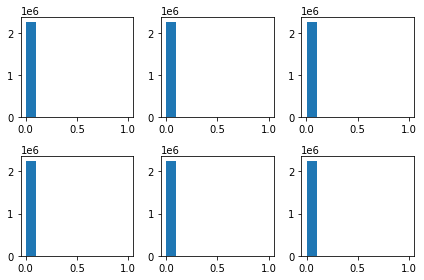
Vamos investigar o que está acontecendo. Como será que estão distribuidas as intensidades dessas imagens?
1
2
3
4
5
6
fig, axs = plt.subplots(2,3)
idx = [(0,0), (0,1), (0,2), (1,0), (1,1), (1,2)]
for i in range(6):
axs[idx[i]].hist(imgs[i].flatten())
plt.tight_layout()
Os histogramas das imagens apontam que a maioria dos pixels possui valor baixo. E agora?
Equalização de histograma
A primeira técnica de processamento de imagens que vamos utilizar é a equalização de histograma, uma técnica que permite aumentar o contraste de imagens.
Essencialmente, queremos transformar uma imagem em k-bits de forma que o histograma fique “reto”, isto é, a probabilidade de obtermos um pixel com intensidade $n_{i}\in[0,I_{max}]$ é mais ou menos a mesma para qualquer $i\in{1,2,…,k}$.
Eu não vou me aprofundar em como fazer isso de fato, mas pretendo escrever sobre no futuro, aguardem!
Em python, podemos escrever uma função razoavelmente simples que toma conta disso:
1
2
3
4
5
6
7
8
9
def hist_eq(img, nbins=2**16):
img_hist, bins = np.histogram(img.flatten(), nbins, density=True)
cdf = img_hist.cumsum()
cdf = (nbins-1) * cdf / cdf[-1]
img_eq = np.interp(img.flatten(), bins[:-1], cdf)
return img_eq.reshape(img.shape)
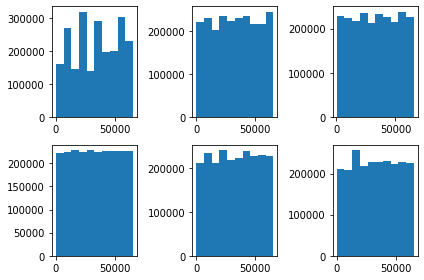
Equalizando os histogramas e verificando os resultados:
1
2
3
4
5
6
7
8
imgs = [np.array(hist_eq(i)) for i in imgs]
fig, axs = plt.subplots(2,3)
idx = [(0,0), (0,1), (0,2), (1,0), (1,1), (1,2)]
for i in range(6):
axs[idx[i]].hist(imgs[i].flatten())
plt.tight_layout()
1
show_img(imgs, 2, 3)
Bem melhor, não? Agora basta colocar uma imagem em cada canal e boom! Mas, espera aí…
Combinando imagens
Bem, temos três canais e seis imagens, algo não cheira bem. E agora? Escolher três e jogar fora metade dessas belas imagens? Desistir e ir chorar no banho? Não! Basta combinar duas imagens em uma! Podemos definir uma nova imagem a partir de duas: sejam duas imagens $M_{1}$ e $M_{2}$ e seus respectivos pixels $p_{ij}^{1}$ e $p_{ij}^{2}$. Definimos $M_{3}$ como a imagems com entradas $p_{ij}^{3} = f(p_{ij}^{1},p_{ij}^{2})$, onde $f:[0,I_{max}]\times[0,I_{max}]\to[0,I_{max}]$ é uma função dos pixels de $M_{1}$ e $M_{2}$. Confuso? Bom, talvez um exemplo facilite: podemos tirar a média pixel por pixel, ou pegar o maior valor. Com certeza existem escolhas melhores de $f$, mas para facilitar as nossas vidas, vamos apenas tirar a média das imagens:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
red = np.dstack([imgs[4],imgs[5]])
red = red.mean(axis=2)
red = (red - red.min())/(red.max() - red.min())
green = np.dstack([imgs[2],imgs[3]])
green = green.mean(axis=2)
green = (green - green.min())/(green.max() - green.min())
blue = np.dstack([imgs[0],imgs[1]])
blue = blue.mean(axis=2)
blue = (blue - blue.min())/(blue.max() - blue.min())
channels = [red, green, blue]
show_img(channels, 1, 3)
Agora, podemos finalmente jogar uma imagem em cada canal e partir pro abraço, certo? Não.
Algoritmo de Lupton
Apesar de representarem as frequências que corresponderiam às cores verde, vermelho e azul, é recomendável ainda preparar as imagens para que elas de fato componham os canais de cor. Um rapaz chamado Lupton propôs um algoritmo que faz essa preparação em imagens astronômicas. Essencialmente, é aplicada uma transformação não-linear(envovendo um arcosseno hiperbólico) corrigida por um fator que nós podemos controlar(que é a verdadeira razão de eu estar colocando isso aqui, já que se você ignorar essa parte, já é possível conseguir um resultado legal, mas estamos aqui para aprender, não é?). Esse método permite distinguir melhor objetos astronômicos ao garantir que objetos com cores específicas possuam uma cor distinta na imagem final. Recomendo a leitura do artigo original, é razoavelmente simples e é muito bem escrito.
Enfim, podemos aplicar esse método assim:
1
2
3
4
5
6
7
8
9
10
11
def asinh(img_src, non_linear=2.0):
img = np.array(img_src, copy=True)
scale_min = img.min()
scale_max = img.max()
factor = np.arcsinh((scale_max - scale_min))
img = np.arcsinh((img - scale_min)/non_linear)/factor
return img
Colorindo a imagem!
Agora, podemos juntar tudo e criar nossa bela imagem da NGC3324:
1
2
3
4
5
6
7
8
9
10
11
12
I = np.mean(channels, axis=0)
new_channels = [channels[0]*asinh(I, non_linear = .99)/I,
channels[1]*asinh(I, non_linear = .99)/I,
channels[2]*asinh(I, non_linear = .99)/I]
new_channels = np.clip(new_channels, 0, 1)
color_img = np.dstack(new_channels)
plt.figure(figsize=(10,10))
ax = plt.subplot()
ax.imshow(color_img, "gray")
ax.set_xticks([])
ax.set_yticks([])
Pronto, temos cores! Você pode fazer algumas coisas agora:
- alterar o argumento
non_lineare obter resultados diferentes; - testar o código em outras imagens de telescópio;
- dormir
Enfim, já falei demais. Até o próximo post(pode e vai demorar)!